✏️ 編集
「Q-Q プロット」って何?
2 つの確率分布の分位数を互いにプロットして,両者がどのくらい類似した確率分布なのかを可視化する手法.
縦軸に調べたい確率分布の分位数,横軸に理論分布の確率密度関数の逆関数をプロットする.分布が類似していれば $y=x$ 的な直前上にプロットされる.
Q-Q プロットの一例:

引用: 【Python】正規分布に従っているかを調べる手法 3 種 | データサイエンス情報局
Q-Q プロットの縦軸,横軸の関係をアニメーションにしたもの:
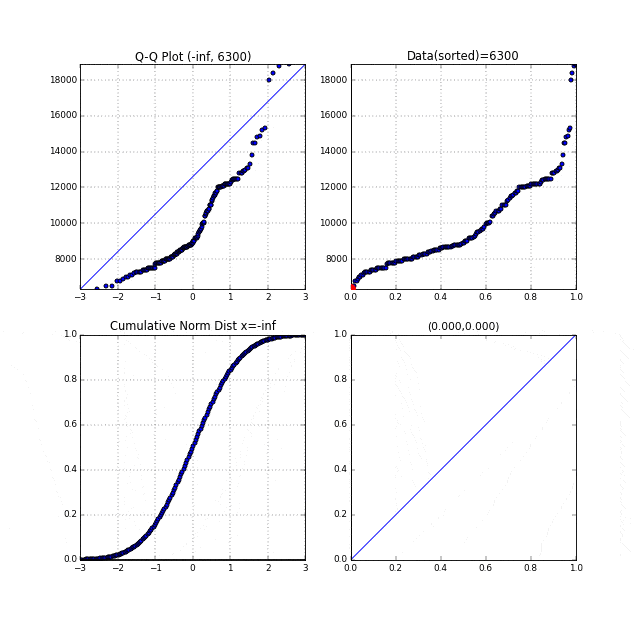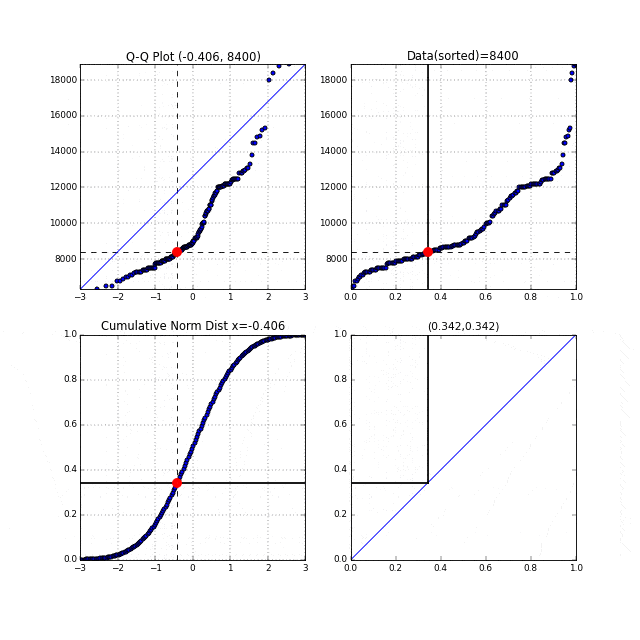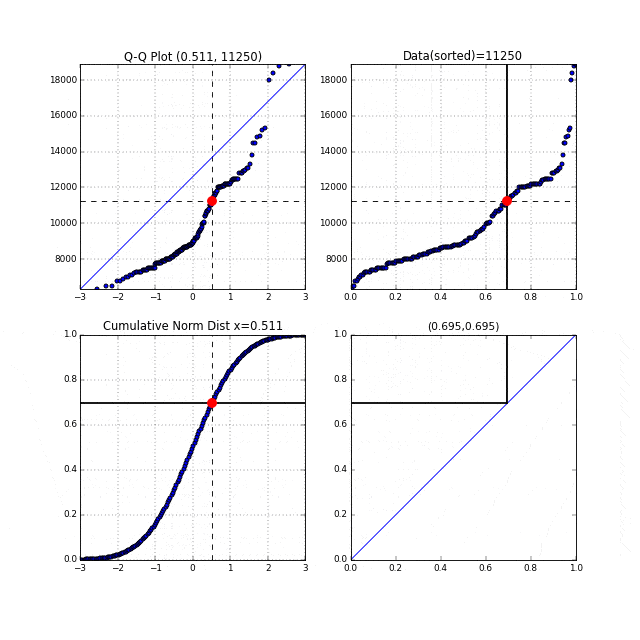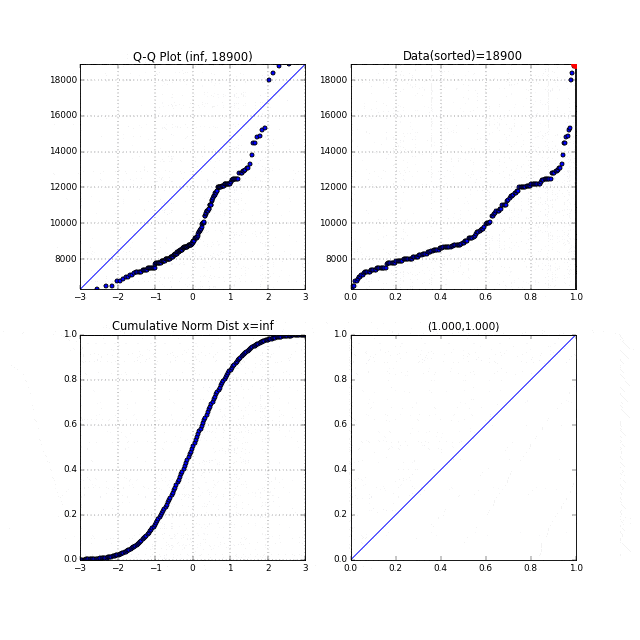
引用: 【統計学】Q-Q プロットの仕組みをアニメーションで理解する。 - Qiita
やってみる
検証コード全体はコチラ:
Google Colab: https://colab.research.google.com/drive/1wSn2s6tbKpCUa6Gbi7zMsIzWZzTCkT_-?usp=sharing
import:
1
2
3
4
5
| import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import scipy.stats as st
from scipy.special import ndtri
|
正規分布からランダムサンプリングしたデータが正規分布と類似しているか調べる
縦軸
サンプリングしたデータのヒストグラム:
1
2
3
4
5
6
7
8
9
10
11
12
| N = 200 # データ件数
MEAN = 10 # 平均
STD = 3 # 標準偏差
data = np.random.normal(loc=MEAN, scale=STD, size=N)
plt.title(f"正規分布からランダムサンプリングしたプロットのヒストグラム\n(平均={MEAN},標準偏差={STD})")
plt.xlabel("階級")
plt.ylabel("度数")
plt.hist(data, bins=20)
plt.grid(True)
plt.show()
|

データの分位数:
1
2
3
4
5
6
7
8
9
10
11
| sorted_data = np.sort(data)
x = np.linspace(0, 1, N)
plt.figure(figsize=(5, 5))
plt.title("正規分布からランダムサンプリングしたプロットの分位数")
plt.xlabel("分位数")
plt.ylabel("値")
plt.xlim(0, 1)
plt.scatter(x, sorted_data)
plt.grid(True)
plt.show()
|

横軸
今回の理論分布は正規分布なので,正規分布の確率密度関数(=正規累積分布関数)の逆関数を用いる.
正規累積分布:
1
2
3
4
5
6
7
8
9
| x = np.linspace(-STD, STD, N)
y_cdf = st.norm.cdf(x)
plt.figure(figsize=(5, 5))
plt.title(f"正規累積分布関数\n(定義域=[{-STD}, {STD}])")
plt.xlabel("x")
plt.ylabel("y")
plt.scatter(x, y_cdf)
plt.grid(True)
|

正規累積分布関数の逆関数:
1
2
3
4
5
6
7
8
9
| x = np.linspace(0, 1, N)
inv_norm = ndtri(x)
plt.figure(figsize=(5, 5))
plt.title(f"正規累積分布関数の逆関数\n(定義域=[{0}, {1}])")
plt.xlabel("x")
plt.ylabel("y")
plt.scatter(x, inv_norm)
plt.grid(True)
|

Q-Q プロット
1
2
3
4
5
6
| plt.figure(figsize=(5, 5))
plt.title(f"Q-Qプロット")
plt.xlabel("理論分布")
plt.ylabel("対象データの分布")
plt.scatter(inv_norm, sorted_data)
plt.grid(True)
|

グラフが一直線になっていることが分かり,対象データの確率分布が正規分布に類似していることが確認できた.
個人的な理解
- 同じ分布なら,ソートして分位数で可視化したときの分布も同じはず
- その場合,同じデータを x 軸,y 軸両方にプロットするのと同じなので,そのプロットは $y=x$ 的な感じになる
- 理論分布の分位数プロットは累積確率関数が使える
- 「なら,理論分布の関数から分位数プロット生成してもいけるのでは?」と思ってやってみたけど,Q-Q プロット生成時の逆関数値が分からなくて詰んだ…
実用
SciPy の stats.probplot() を使えば簡単に Q-Q プロットを作成できる.
1
2
3
4
| fig = plt.subplots(figsize=(5, 5))
st.probplot(sorted_data, dist="norm", plot=plt)
plt.show()
|

参考記事






